Pembelajaran: senin, 9 februari 2026

 

 Assalamualaikum

Selamat datang dikelas 6C semester 2, anak-anak hebat, kelas yang akan menjadi tempat kalian belajar, bermain , dan bertumbuh bersama . Bapak berharap kalian semua dapat menyesuaikan diri dengan kelas baru kalian. Jangan malu bertanya jika ada hal yang belum kalian pahami dan kami akan selalu berusaha membantu kalian untuk belajar dengan baik dan nyaman.bapak juga berharap kalian selalu melaksanan sholat lima waktu tepat pada waktunya dan selalu murojaah surat-surat pendek,agar bertambah selalu hafalan kalian

Matematika (Sumatif ke 1)

• Menghitung volume dan luas permukaan

• Menyelesaikan masalah kontekstual (soal cerita)

1️⃣ KUBUS

🔹 Pengertian

Kubus adalah bangun ruang yang memiliki 6 sisi berbentuk persegi dan semua sisinya sama besar.

🔹 Ciri-ciri Kubus

• 6 sisi (persegi)

• 12 rusuk sama panjang

• 8 titik sudut

• Semua sudut siku-siku

🔹 Rumus Kubus

Misalkan panjang rusuk = s

• Volume

  $$𝑉=𝑠\times 𝑠\times 𝑠={𝑠}^3$$

• Luas Permukaan

  $$𝐿=6\times {𝑠}^2$$

🔹 Contoh Soal

Sebuah kubus memiliki rusuk 5 cm.

• Volume = 5 × 5 × 5 = 125 cm³

• Luas permukaan = 6 × 25 = 150 cm²

2️⃣ BALOK

🔹 Pengertian

Balok adalah bangun ruang yang memiliki 6 sisi berbentuk persegi panjang.

🔹 Ciri-ciri Balok

• 6 sisi (persegi panjang)

• 12 rusuk

• 8 titik sudut

• Memiliki 3 ukuran berbeda: panjang (p), lebar (l), tinggi (t)

🔹 Rumus Balok

• Volume

  $$𝑉=𝑝\times 𝑙\times 𝑡$$

• Luas Permukaan

  $$𝐿=2(𝑝𝑙+𝑝𝑡+𝑙𝑡)$$

🔹 Contoh Soal

Balok dengan p = 10 cm, l = 6 cm, t = 4 cm

• Volume = 10 × 6 × 4 = 240 cm³

• Luas permukaan = 2(60 + 40 + 24) = 248 cm²

3️⃣ JARING-JARING

• Kubus: terdiri dari 6 persegi

• Balok: terdiri dari 3 pasang persegi panjang
  Jaring-jaring dapat dilipat menjadi bangun ruang.

4️⃣ Soal Latihan

1. Sebuah kubus memiliki rusuk 8 cm. Hitung volumenya!

2. Sebuah balok berukuran 12 cm × 5 cm × 4 cm. Hitung luas permukaannya!

3. Sebuah kotak berbentuk balok dapat menampung beras sebanyak berapa cm³?

Menjelaskan makna lokasi suatu objek.
Membaca posisi suatu benda pada denah atau petak koordinat

MATERI 

Membaca dan menentukan lokasi

sistem koordinat kartesius adalah sebuah sistem yang menunjukkan titik-titik dalam sebuah bidang dengan menggunakan beberapa bilangan pada garis koordinat.

Sistem ini umumnya digunakan untuk mengetahui letak atau posisi dari suatu titik atau benda pada suatu bidang. Oleh karena itu, sistem ini banyak dimanfaatkan pada proses pemetaan.

Bidang kartesius adalah sebuah bidang yang di dalamnya terdapat sistem koordinat kartesius, sedangkan sistem koordinat kartesius adalah sebuah sistem yang ada di dalam bidang tersebut.

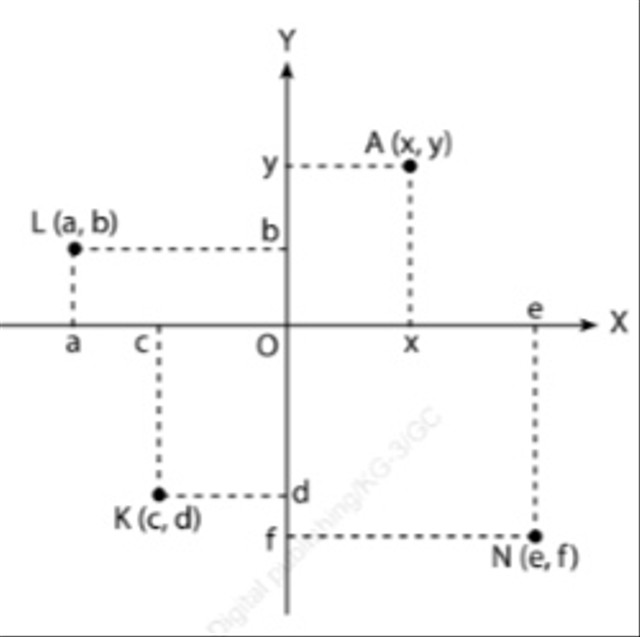
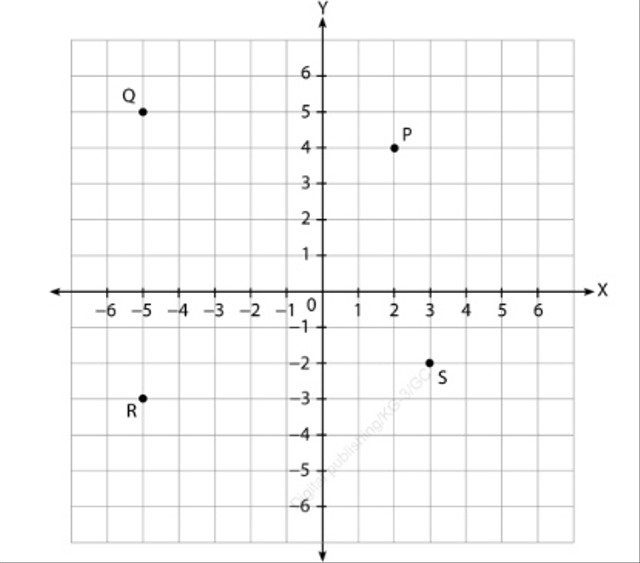
Cara Menentukan Titik Koordinat pada Bidang Kartesius

Untuk menentukan titik koordinat pada bidang kartesius, perhatikan gambar berikut.

Perbesar

Pada bidang kartesius, potongan sumbu x dan y disebut dengan pangkal koordinat. Foto: Buku Kumpulan Materi dan Rumus Matematika SD/MI Kelas 4, 5, 6 karya Muklis

Berdasarkan gambar tersebut, dapat dilihat bahwa:

Sumbu x dan sumbu y berpotongan tegak lurus di titik O. Titik O ini dinamakan pangkal koordinat.
Bilangan-bilangan pada daerah atas x dan daerah kanan y bernilai positif.
Bilangan-bilangan pada daerah bawah x dan daerah kiri y bernilai negatif.
Letak suatu titik koordinat pada bidang kartesius dinyatakan sebagai A(x,y).
Bilangan x pada bidang kartesius disebut absis, sedangkan y adalah ordinat.

Selanjutnya perhatian bidang kartesius di bawah ini.

Perbesar

Ilustrasi bidang kartesius. Foto: Buku Kumpulan Materi dan Rumus Matematika SD/MI Kelas 4, 5, 6 karya Muklis

Cara membaca atau menentukan titik koordinat adalah memperhatikan titik yang searah pada sumbu x dan y.

Contohnya, titik P, titik P terletak pada pertemuan bilangan 2 pada sumbu x dan bilangan 4 pada sumbu y. Maka, titik koordinatnya titik P adalah P(2,4)

Baik terimakasih, cukup sekian pembelajaran kita hari ini. semoga bermanfaat.

Wassalamualaikum, wr.wb.