MATERI AJAR HARI SELASA,20 AGUSTUS 2024
SELAMAT PAGI, TABIK PUN ......
MATERI HARI INI :
KELAS : 6B
Mata pelajaran : Matematika
TUJUAN PEMBELAJARAN- Peserta didik mampu memahami Penjumlahan dan Pengurangan Bilangan Pecahan
- Peserta didik mampu menghitung/mencari Penjumlahan dan Pengurangan Bilangan Pecahan
- Peserta didik mampu mengidentifikasi masalah Penjumlahan dan Pengurangan Bilangan Pecahan
- Peserta didik mampu menyelesaikan masalah Penjumlahan dan Pengurangan Bilangan Pecahan
Bilangan pecahan adalah bilangan yang disajikan a/b dibaca a per b. Di mana a dan b adalah bilangan bulat serta b tidak sama dengan 0 (nol). Bilangan a sebagai pembilang dan bilangan b sebagai penyebut.
- Peserta didik mampu memahami Penjumlahan dan Pengurangan Bilangan Pecahan
- Peserta didik mampu menghitung/mencari Penjumlahan dan Pengurangan Bilangan Pecahan
- Peserta didik mampu mengidentifikasi masalah Penjumlahan dan Pengurangan Bilangan Pecahan
- Peserta didik mampu menyelesaikan masalah Penjumlahan dan Pengurangan Bilangan Pecahan
Bilangan pecahan adalah bilangan yang disajikan a/b dibaca a per b. Di mana a dan b adalah bilangan bulat serta b tidak sama dengan 0 (nol). Bilangan a sebagai pembilang dan bilangan b sebagai penyebut.
1. Pecahan biasa
Pecahan biasa dibagi menjadi dua macam, yaitu pecahan sejati dan pecahan tidak sejati.- Pecahan sejati merupakan bilangan pecahan yang pembilangnya lebih kecil daripada penyebutnya.
- Pecahan tidak sejati merupakan kebalikannya. Misalkan diketahui sebuah bilangan pecahan a/b, jika a < b disebut pecahan sejati, jika a > b disebut pecahan tidak sejati.
Contoh:
- Pecahan sejati merupakan bilangan pecahan yang pembilangnya lebih kecil daripada penyebutnya.
- Pecahan tidak sejati merupakan kebalikannya. Misalkan diketahui sebuah bilangan pecahan a/b, jika a < b disebut pecahan sejati, jika a > b disebut pecahan tidak sejati.
2. Pecahan campuran
Pecahan campuran adalah pecahan yang memuat campuran bilangan bulat dan pecahan murni. Pecahan campuran diperoleh dari pecahan biasa tidak sejati dengan pembagian porogapit bersisa.
Contoh:

- Cara Mengubah Pecahan Biasa (Tidak Murni) ke Pecahan Campuran
Pembilang dibentuk menjadi kelipatan penyebut, dan ditambahkan sisanya.
Contoh:
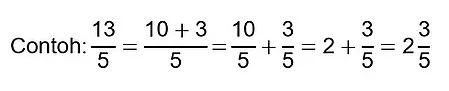
(gambar Ruang Guru)
Atau cara menggunakan porogapit:
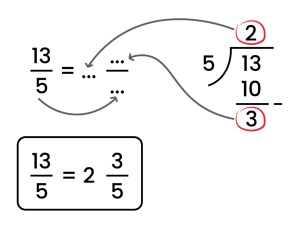
(cara porogapit gambar: Ruang Guru)
- Cara Mengubah Pecahan Campuran ke Pecahan Biasa (Tidak Murni)
Pembilang dibentuk dari bilangan bulat pada pecahan campuran yang dikalikan dengan penyebut, lalu ditambahkan pembilang pada pecahan campuran.
Contoh:
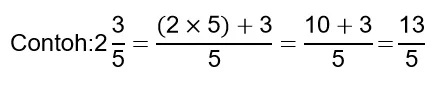
Pecahan campuran adalah pecahan yang memuat campuran bilangan bulat dan pecahan murni. Pecahan campuran diperoleh dari pecahan biasa tidak sejati dengan pembagian porogapit bersisa.
Contoh:

Contoh:

- Cara Mengubah Pecahan Biasa (Tidak Murni) ke Pecahan Campuran
Pembilang dibentuk menjadi kelipatan penyebut, dan ditambahkan sisanya.
Contoh:
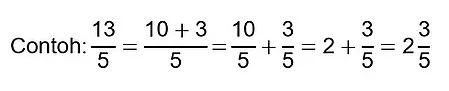
(gambar Ruang Guru)
Atau cara menggunakan porogapit:

(cara porogapit gambar: Ruang Guru)
- Cara Mengubah Pecahan Campuran ke Pecahan Biasa (Tidak Murni)
Pembilang dibentuk dari bilangan bulat pada pecahan campuran yang dikalikan dengan penyebut, lalu ditambahkan pembilang pada pecahan campuran.
Contoh:
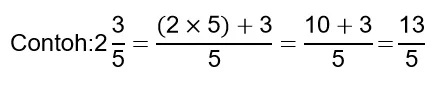
3. Pecahan Desimal
Pecahan desimal merupakan bilangan pecahan yang penyebutnya bilangan kelipatan 10, yaitu 10, 100, 100, dst. Penulisan dari bilangan ini menggunakan tanda koma (,).
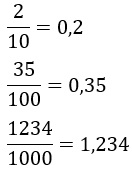
Pecahan desimal merupakan bilangan pecahan yang penyebutnya bilangan kelipatan 10, yaitu 10, 100, 100, dst. Penulisan dari bilangan ini menggunakan tanda koma (,).
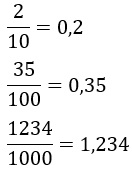
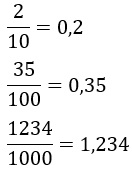
4. Pecahan Senilai
Pecahan senilai merupakan dua atau lebih bilangan pecahan yang memiliki perbandingan yang sama antara pembilang dan penyebutnya.
Contoh:
1/2 senilai dengan 4/8, karena perbandingan pembilang dan penyebutnya sama, yaitu 1/2.
Pecahan senilai merupakan dua atau lebih bilangan pecahan yang memiliki perbandingan yang sama antara pembilang dan penyebutnya.
Contoh:
1/2 senilai dengan 4/8, karena perbandingan pembilang dan penyebutnya sama, yaitu 1/2.





Komentar
Posting Komentar