Pembelajaran: senin,25 agustus 2025

-



 Assalamualaikum
Selamat datang dikelas 6C anak-anak hebat, kelas yang akan menjadi tempat kalian belajar, bermain , dan bertumbuh bersama selama satu tahun ke depan. Bapak berharap kalian semua dapat menyesuaikan diri dengan kelas baru kalian. Jangan malu bertanya jika ada hal yang belum kalian pahami dan kami akan selalu berusaha membantu kalian untuk belajar dengan baik dan nyaman.bapak juga berharap kalian selalu melaksanan sholat lima waktu tepat pada waktunya dan selalu murojaah surat-surat pendek,agar bertambah selalu hafalan kalian.

Sumatif 1

Bahasa Indonesia
Tujuan Pembelajaran
Murid dapat memahami informasi dan kosakata baru yang          memiliki makna denotatif, konotatif, dan kiasan untuk mengidentifikasi objek, fenomena, dan karakter

Materi Pembelajaran

A. Pengertian Kosakata Berdasarkan Makna

Jenis MaknaPenjelasanContoh
DenotatifMakna yang sebenarnya atau lugas, sesuai kamus."Ia menulis di papan tulis."
KonotatifMakna tambahan, bersifat emosional atau nilai rasa, tergantung konteks."Ia adalah buaya darat." (artinya: lelaki yang suka mempermainkan wanita)
Kiasan (Majas)Makna tidak langsung, bersifat perbandingan atau simbolik."Wajahnya secantik rembulan." (perbandingan/kiasan)

🧾 B. Kosakata Baru dalam Konteks

  1. Identifikasi makna melalui konteks kalimat:

    • Kalimat: “Badai emosi melanda dirinya setelah mendengar kabar itu.”
      → Kosakata baru: badai emosi
      → Makna: perasaan yang sangat kacau atau marah hebat (kiasan)

  2. Gunakan strategi memahami kosakata baru:

    • Baca seluruh kalimat.

    • Cermati kata-kata sekitar.

    • Tentukan apakah maknanya literal atau tidak.

    • Jika perlu, cari di kamus.

🔍 C. Penerapan: Mengidentifikasi Objek, Fenomena, dan Karakter

1. Objek

Gunakan kosakata bermakna denotatif dan konotatif untuk menggambarkan objek secara lebih ekspresif.

Contoh:

  • Denotatif: Pohon itu besar dan rindang.

  • Konotatif: Pohon itu seperti penjaga setia halaman rumah.

2. Fenomena

Fenomena alam atau sosial bisa digambarkan dengan kosakata kiasan agar lebih hidup.

Contoh:

  • Denotatif: Angin kencang melanda desa.

  • Kiasan: Angin amarah alam menyapu desa kecil itu.

3. Karakter

Karakter tokoh dalam cerita bisa dihidupkan dengan penggunaan makna konotatif/kiasan.

Contoh:

  • Denotatif: Ia adalah guru yang tegas.

  • Konotatif/kiasan: Ia adalah singa di kelas, disegani dan ditakuti.

📝 D. Latihan Pemahaman

Latihan 1: Identifikasi Makna

Tentukan makna kata berikut dalam kalimat!

  1. "Ia memikul beban hidup yang berat." → Makna kata beban hidup?

  2. "Wajahnya bersinar saat menerima penghargaan." → bersinar makna denotatif atau konotatif?

  3. "Jantung kota mulai berdetak lagi setelah pandemi." → Apa arti jantung kota dan berdetak di sini?

Latihan 2: Ubah Kalimat

Ubah kalimat bermakna denotatif menjadi konotatif/kiasan!

  1. Denotatif: "Ia sangat pintar."
    → Konotatif/kiasan: "Ia otaknya encer seperti ilmuwan."

  2. Denotatif: "Mereka bekerja keras setiap hari."
    → Kiasan: "Mereka membanting tulang demi sesuap nasi."

✨ Penutup dan Refleksi

Memahami makna kata lebih dari sekadar arti kamus:

  • Makna denotatif penting untuk kejelasan.

  • Makna konotatif memperkaya ekspresi.

  • Makna kiasan menciptakan daya imajinasi dan estetika bahasa.

🗣 Pertanyaan Reflektif:

  • Kapan kamu harus menggunakan makna denotatif?

  • Apa keuntungan memahami makna konot

Matematika

Tujuan Pembelajaran

Membandingkan dan mengurutkan berbagai pecahan termasuk pecahan campuran, melakukan operasi penjumlahan dan pengurangan pecahan, serta melakukan operasi perkalian dan pembagian pecahan dengan bilangan asli

Materi

Mengidentifikasi dan membedakan pecahan biasa, pecahan campuran,   pecahan desimal, dan persen

Secara matematis, bilangan pecahan dapat disimbolkan dengan “a/b”. Bilangan a/b bisa dibaca dengan “a per b”. Bilangan a sebagai pembilang dan bilangan b sebagai penyebut.

Jenis-Jenis Bilangan Pecahan

Tahukah kamu terdapat berapa jenis bilangan pecahan?

Bilangan pecahan terbagi menjadi 4 jenis, yaitu : pecahan biasa, pecahan campuran, pecahan desimal, dan pecahan senilai.

1. Pecahan Biasa

Pecahan biasa terbagi menjadi dua macam, yaitu pecahan sejati dan pecahan tidak sejati. Pecahan sejati merupakan bilangan pecahan yang pembilangnya lebih kecil daripada penyebutnya. Sedangkan pecahan tidak sejati merupakan kebalikannya. Misalkan diketahui sebuah bilangan pecahan a/b, jika a < b disebut pecahan sejati, jika a > b disebut pecahan tidak sejati.

Contoh :

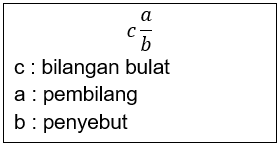
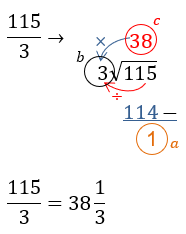
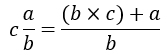
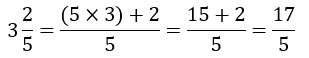
image article

2. Pecahan Campuran

Pecahan campuran dapat diperoleh dari pecahan biasa tidak sejati dengan pembagian porogapit bersisa. Pecahan campuran terdiri dari bilangan bulat dan bilangan pecahan biasa. Pecahan campuran dapat disimbolkan sebagai berikut:

image article

Cara mengubah pecahan biasa ke pecahan campuran dapat dilakukan dengan menggunakan cara porogapit. Contoh :

image article

Selain mengubah pecahan biasa ke pecahan campuran, kalian juga bisa mengubah pecahan campuran ke pecahan biasa dengan cara berikut:

image article

Contoh:

image article

3. Pecahan Desimal

Pecahan desimal merupakan bilangan pecahan yang penyebutnya bilangan kelipatan 10, yaitu 10, 100, 100, dst.  Penulisan dari bilangan ini menggunakan tanda koma (,). Contoh :

image article

3. Pecahan Senilai

Pecahan senilai merupakan dua atau lebih bilangan pecahan yang memiliki perbandingan yang sama antara pembilang dan penyebutnya.

Contoh:

1/2 senilai dengan 4/8, karena perbandingan pembilang dan penyebutnya sama, yaitu 1/2.

Persen adalah pecahan yang penyebutnya seratus dan dilambangkan dengan (%). Agar lebih paham mengenai cara mencari persen dari angka, berikut adalah contoh soal yang dikutip dari Buku Matrikulasi Matematika Dasar untuk Tingkat Perguruan Tinggi yang ditulis oleh Samuel Rex Mulyadi, dkk:
1. Jumlah seluruh siswa kelas III SD Mutu Tanah sebanyak 20 orang. Laki-laki 12 orang dan perempuan 8 orang. Tentukan persentase dari jumlah laki-laki!
Jawab: Persentase = Jumlah siswa yang diketahui/jumlah seluruh siswa x 100
Persentase = 12/20 x 100
Persentase = 1200/20

Persentase = 60% 


Kesimpulan dan refleksi: 

Di hari ini sisea berfokus pada pengerjaan sumatif 1 bahasa infonesia

Dari soal yg di kerjakan siswa memerlukan waktu yg lebih dr yg di sedikan dikarenakan soal yg terlalu HOTS dan untuk pembahasan dilakukan di hari berikutnya.

Untuk matematika siswa mepelajari perkalian pecahan dan pembagian pecajan dan bentuk sederhana dari hasil operaasi pecahan.





Komentar

Posting Komentar

Postingan populer dari blog ini

KISI KISI PENILAIAN AKHIR SEMESTER GANJIL : TEMA 1

-
Gambar
   SELAMAT PAGI, TA BIK PUN ...... Selamat pagi,,,,Tabik pun Assalamualaikum.wr.wb anak sholeh/sholeha VI B , apa kabar hari ini?Alhamdulillah semoga kita semua selalu sehat dan selalu dalam lindungan Allah SWT.aamiin ya Robbal allamin. Jangan lupa sebelum belajar dengarkan tausiah dan rangkum isinya kemudian tadarus dan shalat dhuha   Pada hari ini ananda akan melaksanakan PTS TEMA 1 DAN PAI. Bu Guru harap ananda semua mempelajari lagi materi-materi yang sudah Bu Guru berikan dengan teliti.  Tugas ananda sholeh sholeha yaitu mempelajari kisi-kisi Tema 2 untuk persiapan PTS. Di bawah ini kisi-kisinya ya nak: KISI-KISI PAS TEMA 2 :   Persatuan dan Kesatuan Disajikan beberapa perilaku, siswa dapat menentukan perilaku menumbuhkan persatuan dan kesatuan Persatuan dan Kesatuan Disajikan sebuah ilustrasi , siswa dapat memilih sikap tepat yang seharusnya dilakukan siswa dalam menghormati perbedaan Persatuan dan Kesatuan Disajikan sebuah gambar, siswa dapat memilih sika...
Baca selengkapnya

pembelajaran: jum'at, 19 september 2025

-
Gambar
      Assalamualaikum Selamat datang dikelas 6C anak-anak hebat, kelas yang akan menjadi tempat kalian belajar, bermain , dan bertumbuh bersama selama satu tahun ke depan. Bapak berharap kalian semua dapat menyesuaikan diri dengan kelas baru kalian. Jangan malu bertanya jika ada hal yang belum kalian pahami dan kami akan selalu berusaha membantu kalian untuk belajar dengan baik dan nyaman.bapak juga berharap kalian selalu melaksanan sholat lima waktu tepat pada waktunya dan selalu murojaah surat-surat pendek,agar bertambah selalu hafalan kalian Mapel Seni Rupa Pembelajaran Seni Rupa latihan soal  Makrame adalah karya seni tangan  (handmade)  untuk menggabungkan simpul yang terdiri atas beberapa tali atau benang. Karya seni makrame dapat berupa hiasan atau barang siap pakai. selamat mengerjakan soal  Soal Isian – Kerajinan Makramé Kelas 6 SD Makramé adalah kerajinan tangan yang dibuat dengan cara menyusun tali melalui teknik __________. Simpul da...
Baca selengkapnya

Pembelajaran: senin, 1 september 2025

-
Gambar
    Assalamualaikum Selamat datang dikelas 6C anak-anak hebat, kelas yang akan menjadi tempat kalian belajar, bermain , dan bertumbuh bersama selama satu tahun ke depan. Bapak berharap kalian semua dapat menyesuaikan diri dengan kelas baru kalian. Jangan malu bertanya jika ada hal yang belum kalian pahami dan kami akan selalu berusaha membantu kalian untuk belajar dengan baik dan nyaman.bapak juga berharap kalian selalu melaksanan sholat lima waktu tepat pada waktunya dan selalu murojaah surat-surat pendek,agar bertambah selalu hafalan kalian. Mapel Matematika Tujuan Pembelajaran Membandingkan dan mengurutkan berbagai pecahan termasuk pecahan campuran, melakukan operasi penjumlahan dan pengurangan pecahan, serta melakukan operasi perkalian dan pembagian pecahan dengan bilangan asli Materi Mengurutkan berbagai pecahan (pecahan biasa, pecahan campuran, desimal, dan persen) Mapel Matematika Tujuan Pembelajaran Membandingkan dan mengurutkan berbagai pecahan termasuk pecahan campur...
Baca selengkapnya